前言
本文主要介绍Top-Tree、Euler-Tour-Tree+LCT和一种奇怪的未命名的动态树。
Top-Tree
简介
这是什么?
一种Link-Cut-Tree的拓展,以维护子树信息著称。
另说应该叫AAA树。事实上作者我也不是很懂这一套理论,反正叫Toptree大家都知道是啥,就这么叫了吧qwq
(Tarjan论文里还给加了个修饰“自适应”,事实上你问我辛普森和自适应辛普森的区别是什么,我也不知道>.<)
引入
我们该如何动态维护子树信息?先从一种动态树的解决方式——Link-Cut-Tree(LCT)的复杂度证明说起。
首先大家应该都会LCT和树链剖分,不会的还请先不要看这篇文章。
以下证明部分参考杨哲的集训队作业《QTREE解法的一些研究》。
Link-Cut-Tree的复杂度分析
我们知道LCT和树链剖分都有轻重链之分,然而LCT的轻重链是动态变化的,树剖却不是。
我们先把一棵树树链剖分,定义轻边为不在重链上的边,重边为在重链上的边。再对LCT做定义,一个节点在重链【此处的重链为LCT的动态重链,和树剖无关】上的直接儿子定义为preferred child,连向该儿子的边定义为preferred edge。
在LCT的access操作中,我们只要证明preferred child的更改次数是均摊$O(n\log n)$ 的,就可以先证明其复杂度上界为$O(n\log^2 n)$。
现在证明preferred child的更改次数是均摊$O(n\log n)$ 的,首先我们知道一次access最多让$O(\log n)$ 条轻边变为preferred edge,然而重边一次却会有很多变为preferred edge,那么复杂度就是重边变为preferred edge的次数,而重边变为preferred edge的次数级别等于重边从preferred edge变为非preferred edge+所有边【即$n-1$】,那么复杂度就是重边从preferred edge变为非preferred edge的次数,对于一条重边,变为非preferred edge以后,意味着有一条轻边变为preferred edge【或者preferred edge消失,这种情况最多只有$O(q)$个,$q$为access次数】,于是重边从preferred edge变为非preferred edge的次数至多为轻边变为preferred edge的次数,而轻边变为preferred edge的次数显然是$O(n\log n)$的,得证。
其实到这里就可以引入TopTree了,为了完整顺便把splay维护的LCT复杂度是也证了。
现在证明splay维护的LCT复杂度是$O(\log n)$的,首先splay的单次旋转的复杂度是均摊$O(\log sz_{root} - \log sz_x )$,$root$是splay的根,$x$是提根的节点,$sz_x$是$x$子树大小。这个复杂度的证明详见splay的复杂度证明,证明涉及对双旋splay的每一种操作的分析,通过缩放最后还有3的常数,非常麻烦,这里不证了。
然后我们代入access中分析,很容易发现中间的加减相互抵消了,最后的复杂度是均摊$O(\log n - \log sz_x)$。
至此我们完成了LCT的复杂度分析。
Top-Tree的操作分析
那么我们要维护子树信息,该怎么办?
preferred child的更改次数是均摊$O(n\log n)$,这个性质非常优秀,很多动态树题目都通过这个性质来维护各种信息,TopTree也是这样。
考虑在access的时候顺便维护轻儿子的信息,这样就可以动态维护子树信息了。
说白了TopTree其实就没了,因为剩下的就是子树和链之间互相影响的细节了,好好地写一下就能自己处理掉了。
如果儿子无序,那么我们可以直接维护一个二叉树来维护那些轻儿子,如果儿子有序,那么同样可以维护一个BST来维护轻儿子。
每次access进行preferred child更改的时候,考虑轻重边的更改,把要变成轻儿子的重儿子加入维护轻儿子的数据结构,把要变成重儿子的轻儿子从维护轻儿子的数据结构中拿出,放入LCT本身有的维护链的splay中。
这样就完成了access操作,但是打标记的时候会特别恶心,但是无论如何,遵循“轻重分开”的原则进行维护一定没有错的,也就是子树信息管子树信息维护,链信息管链信息维护,当然根据需要,有时候子树信息需要加到链信息上去维护。
(然后sone1的10kb就是这样出来的= =。。)
Top-Tree的复杂度分析
关于LCT原有部分复杂度无需证明了,所需要证明的就是维护轻儿子的复杂度。
这个部分还不会…… 有兴趣的人可以自己去看看论文。
Euler-Tour-Tree
简介
一种从简到烦皆可的维护树形态的数据结构,现先讲Euler-Tour序。
可分需要有好几种写法:
- 不省略Euler-Tour序
- 省略Euler-Tour序为单括号dfs序
省略Euler-Tour序为括号匹配dfs序
其中第一种一般不用于动态树维护。
不省略Euler-Tour序
感觉就只能方便求LCA了,可以比较轻松地做到在线$O(n\log n)-O(1)$不修改求LCA,ST表记深度即可。
经测试这玩意跑特快,蛮有实用价值的,比那啥$O(n)-O(1)$LCA有用。
不过和本主题无关。
省略Euler-Tour序为单括号dfs序
一般只是下一种实现方法的简略版,如果我们不需要链信息,可以不记录括号匹配。
省略Euler-Tour序为括号匹配dfs序
可支持基本操作:
子树操作
换父亲
链询问
以上操作直接使用BST维护dfs序即可,复杂度均为$O(n \log n)$。
通过和LCT结合可以把复杂度提升一个$\log n$来换取链修改的功能。
基本操作:access
在LCTaccess的时候把重儿子表示的子树dfs序拼接到父亲表示的dfs序首,这样就能通过$O(\log^2 n)$的时间得到一个点到根这么一条链上的连续信息。
复杂度$O(n \log^2 n)$
这样我们可以实现链修改了。
然而相较TopTree,如何实现换根?
换根
这种换根方式参考松爷的方式,在ZJOI2015day1的课件中有提及。
我们考虑不管括号匹配的左右关系,如何换根。
那么我们只需要把需要换根的节点x access,然后如下图。
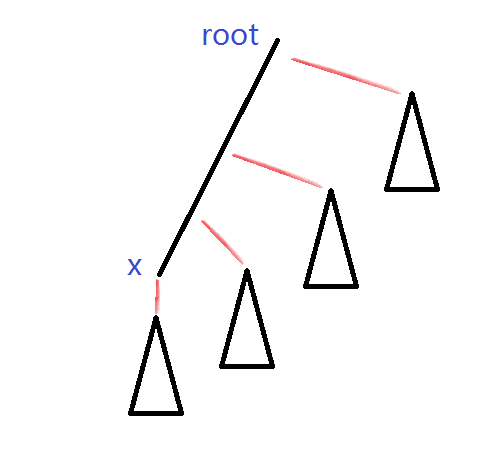
设access以后x所处位置是p,那么reverse(1,p),reverse(p+1,n*2)
这样关系就对了,但是那些红边连向的子树内部左右括号全反了,怎么办呢。
也很简单,直接在LCT上打个标记,下次遇到的时候直接把子树翻转回来就行了,不过这样链询问的复杂度也变为了$O(n\log^2 n)$【这么说起来直接写单括号算了】
复杂度当然也是$O(n\log^2 n)$
至此,ETT基本完成了TopTree的所有操作,只不过……杂度多了一些。。事实上,他跑得确实比TopTree慢。
Q:所以说这种数据结构并没有什么卵用?
A:不!他能衬托TopTree是有用的!
树上动态联通块问题
引入
我们从一个经典的问题开始。
QTREE7:每个点有黑白两种颜色。三种操作。
单点修改颜色
单点修改权值
询问连通块最大权值
解法有很多,我现在比较了解的有两种。
TopTree强行维护异色子树信息,涉及link、cut
既然TopTree可行,我们可以考虑ETT的思路,利用dfs序,方法如下:
显然,一个连通块是可以用dfs序表示的,那么将一个节点的信息存于其深度最低的与其异色的祖先内【根节点特判】,也就是说每个节点存着异色子连通块信息,设这个信息为S(x)
考虑修改节点x的颜色的时候如何操作:
首先将dfs序中其同色连通块儿子取出,变为新的S(x),将原本的S(x)塞入该节点同色连通块的dfs序中。
如果修改节点颜色后颜色与其父亲不一致,那么先前其一定在非直接父亲的祖先的S(x)内,那么从那个祖先内取出,存入直接父亲的S(x)内。若修改节点颜色后颜色与其父亲一致,那么先前其一定在直接父亲的S(x)内,从中取出存入直接父亲所在连通块的dfs序中。
这样我们就成功动态维护了dfs序,dfs序都维护了,max当然不在话下。
如果我们把点修改颜色,换成链修改颜色呢?
我们把问题一般化:链修改+维护联通块dfs序
Link-Cut-Memphis
简介
一种解决树上动态联通块链修改问题的方式。
不知道该叫什么,那就大言不惭地和校内人一起叫LCM算了。
正文
①首先明确一下链修改=一个点到根路径上一个点的区间修改,很显然,找出LCA就行了
②并且在这个区间里,设每个节点颜色为$a_1,a_2,…,a_N$ ,对于$1\leqslant i<N, a_i \not = a_{i+1}$,我们称为一个颜色更变处,设每次操作$i$经过$cnt_i$个颜色更变处,那么 $\sum_{i=1}^{m}{cnt_i}$ 是 $O(m\log n)$级别的,复杂度证明同LCT的preferred-child更变次数的证明。
明确了以上两点后,我们回顾一下QTREE7的解决方法。
首先是Top-Tree,我认为直接上是不能做的,至少我不会,sone爷也不会。
顺着方法2的思路,当然直接上也是不能做的,但是可以看看方法2都维护了什么:
异色子联通块信息
Q:为什么要维护这个东西? A:为了方便维护一个点颜色翻转后处于什么联通块这一需求。
如法炮制,我们知道了②,也就是说暴力求该每个相同的颜色段复杂度是对的,但是我们要维护一条同色链颜色翻转后处于什么联通块。所以,我们需要维护的不仅仅是子联通块了,我们还需要更多。
现颜色以白色和黑色为例,比如有这么一棵树,节点地颜色只有黑白两种,我们分别维护黑树和白树,相对地定义主树和辅树。
定义
一个维护同色联通块信息,可视为一个dfs序表示的同色联通块,称之为主树
——用来维护一条链不变颜色,处于哪个联通块
一个维护异色联通块信息,可视为一个LCT串起来的异色子联通块的dfs序,称之为辅树
——用来维护一条链变了颜色,处于哪个联通块
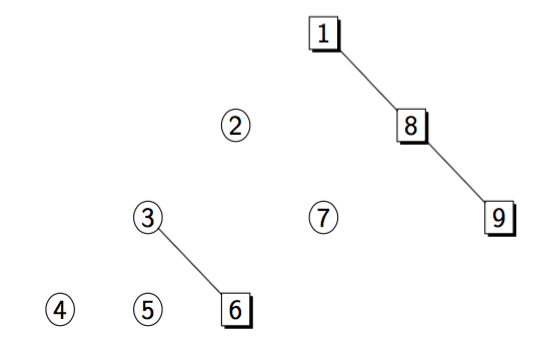
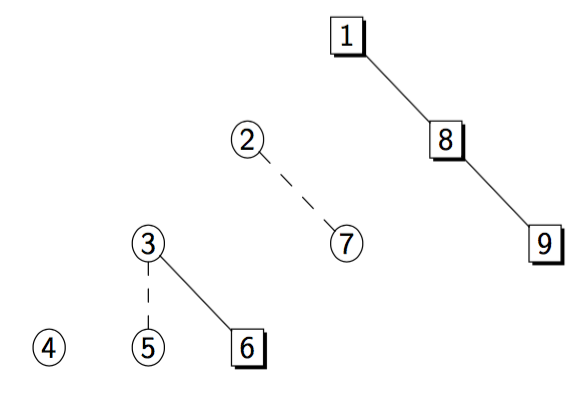
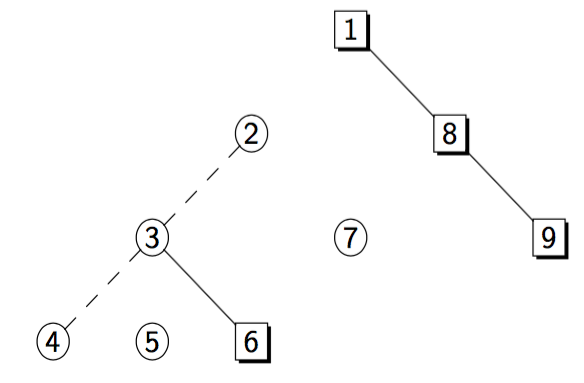
以下是几种可能的黑树形态,其中方块表示黑点,圆表示白点,实边表示在同一个dfs序内,是主树构成,虚边表示在LCT中相连,是父联通块的辅树构成。
注意:一个联通块的主树是构成其父联通块的辅树的一部分
expose操作
定义expose操作为access操作在辅树上的变种操作:
expose一个点,将其到该联通块顶端打通,然后将所有异色联通块dfs序串起来。
*定义expose后所发现的联通顶端节点为关键节点。
expose后将该联通块辅树关键节点所在dfs序接入关键节点父亲所在的主树中,和父联通块主树合并;相对的,将主树中的关键节点从关键节点父亲的辅树中该父亲节点所代表的异色子联通块dfs序中切除,成为父联通块辅树的一部分。
至此,我们可以发现通过expose及其之后的操作,使得该联通块的一条链完成与父联通块的合并,并且原本的主树变为辅树,辅树变为主树。
思路大致明朗。
所谓链修改操作即为将一个节点到根上的一段进行主树和辅树的相互变换。
当然还有很多细节,比如根节点所在联通块要特判之类的。
复杂度上界$O(n\log^2 n)$
至此我们就可以维护链修改+维护联通块dfs序了。
结尾及reference
以上,是我在OI届最后一份学术性文章,从is-programmer转载而来,借用了Stilwell在NOI冬令营上pdf的图片。
感谢观看,如有错误欢迎指出。